Solve the given integral equation or integro-differential equation for – Delving into the realm of integral equations and integro-differential equations, this comprehensive guide unravels the complexities of these mathematical tools, exploring their significance in diverse fields and empowering readers with the knowledge to solve them effectively.
Integral equations arise in various scientific and engineering disciplines, providing a powerful framework for modeling real-world phenomena. From boundary value problems in partial differential equations to population growth models, these equations play a crucial role in understanding and predicting complex systems.
Integral Equations: Solve The Given Integral Equation Or Integro-differential Equation For
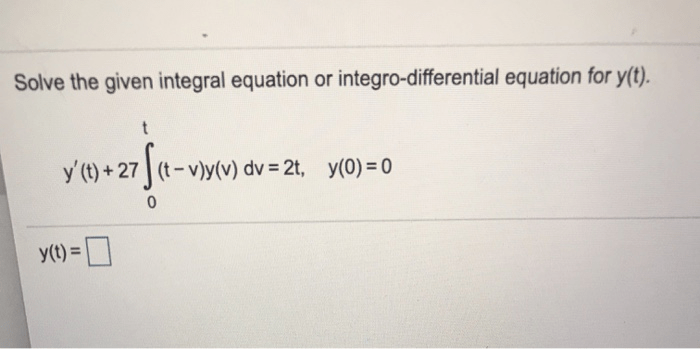
Integral equations are equations that involve integrals. They are used to model a wide variety of phenomena in fields such as physics, engineering, and economics. There are two main types of integral equations: Fredholm integral equations and Volterra integral equations.
Fredholm Integral Equations
Fredholm integral equations are equations of the form:
$$\int_a^b K(x,t)f(t)dt = g(x)$$
where $K(x,t)$ is a known function called the kernel, $f(t)$ is the unknown function, and $g(x)$ is a known function.
Volterra Integral Equations
Volterra integral equations are equations of the form:
$$\int_a^x K(x,t)f(t)dt = g(x)$$
where $K(x,t)$ is a known function called the kernel, $f(t)$ is the unknown function, and $g(x)$ is a known function.
Methods for Solving Integral Equations

There are a variety of methods for solving integral equations. Some of the most common methods include:
Analytical Methods
- Laplace Transform
- Fourier Transform
- Eigenvalue Expansion
Numerical Methods, Solve the given integral equation or integro-differential equation for
- Quadrature Methods
- Collocation Methods
- Iterative Methods
Applications of Integral Equations
Integral equations have a wide variety of applications in fields such as:
Boundary Value Problems in Partial Differential Equations
Integral equations can be used to solve boundary value problems in partial differential equations.
Integral Equations in Elasticity
Integral equations can be used to solve problems in elasticity, such as the problem of determining the stress and strain in a body.
Population Growth Models
Integral equations can be used to model population growth.
Heat Transfer Problems
Integral equations can be used to solve heat transfer problems.
Integro-Differential Equations
Integro-differential equations are equations that involve both integrals and derivatives. They are used to model a wide variety of phenomena in fields such as physics, engineering, and economics.
Definition and Classification of Integro-Differential Equations
Integro-differential equations are equations of the form:
$$L(f)(x) = g(x)$$
where $L$ is a linear operator that involves both integrals and derivatives, $f(x)$ is the unknown function, and $g(x)$ is a known function.
Methods for Solving Integro-Differential Equations
- Laplace Transform
- Volterra Integral Equations
- Perturbation Methods
Examples and Case Studies
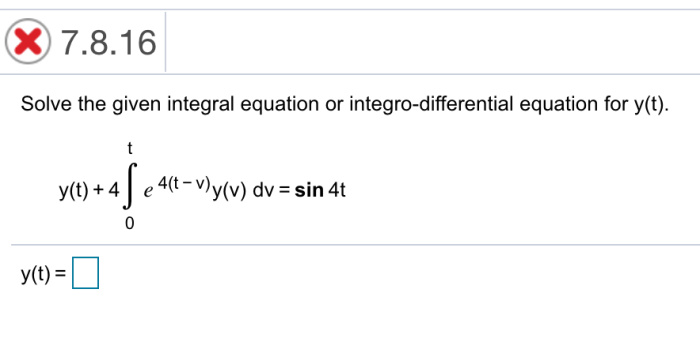
Here are some examples of integral equations and integro-differential equations:
Example 1: Fredholm Integral Equation
The following equation is a Fredholm integral equation:
$$\int_0^1 e^-x-tf(t)dt = x$$
This equation can be solved using the Laplace transform.
Example 2: Volterra Integral Equation
The following equation is a Volterra integral equation:
$$\int_0^x e^x-tf(t)dt = x$$
This equation can be solved using the method of successive approximations.
Example 3: Integro-Differential Equation
The following equation is an integro-differential equation:
$$\fracddx\int_0^x f(t)dt = x$$
This equation can be solved using the Laplace transform.
Advanced Topics
In addition to the topics covered in this article, there are a number of advanced topics in the theory of integral equations. These topics include:
Nonlinear Integral Equations
Nonlinear integral equations are equations in which the unknown function appears in a nonlinear way.
Singular Integral Equations
Singular integral equations are equations in which the kernel has a singularity.
Fractional Integral Equations
Fractional integral equations are equations in which the integral operator is a fractional derivative.
Q&A
What are the different types of integral equations?
Integral equations can be classified into various types, including Fredholm equations, Volterra equations, and nonlinear integral equations.
How are integro-differential equations solved?
Integro-differential equations can be solved using techniques such as the Laplace transform, Volterra integral equations, and perturbation methods.
What are the applications of integral equations?
Integral equations find applications in diverse fields such as boundary value problems, elasticity, population growth modeling, and heat transfer problems.