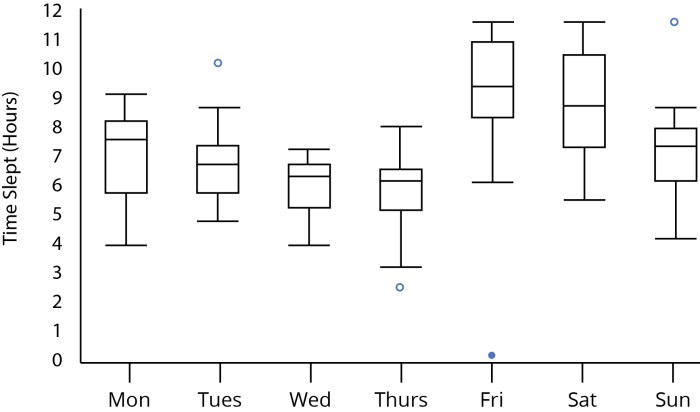
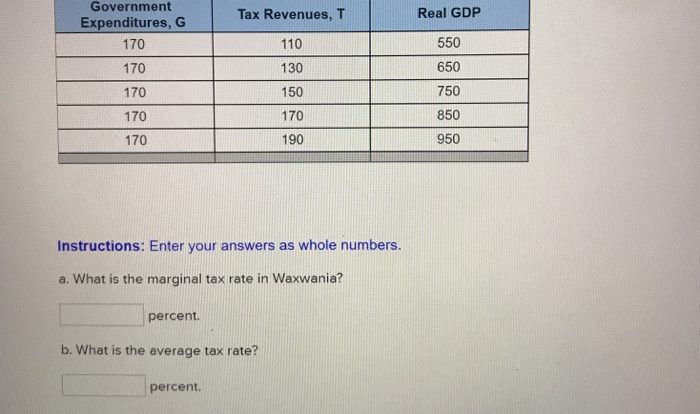
Introducing the Box and Whisker Plot Worksheet 2 Answer Key, a meticulously crafted resource that empowers learners with a comprehensive understanding of this fundamental statistical tool. This guide unravels the intricacies of box and whisker plots, equipping readers with the knowledge to effectively analyze and interpret data.
Delving into the core concepts, we define box and whisker plots, exploring their components and significance. Step-by-step instructions guide users through the process of creating these plots, accompanied by illustrative examples that solidify understanding.
Box and Whisker Plots: A Comprehensive Overview
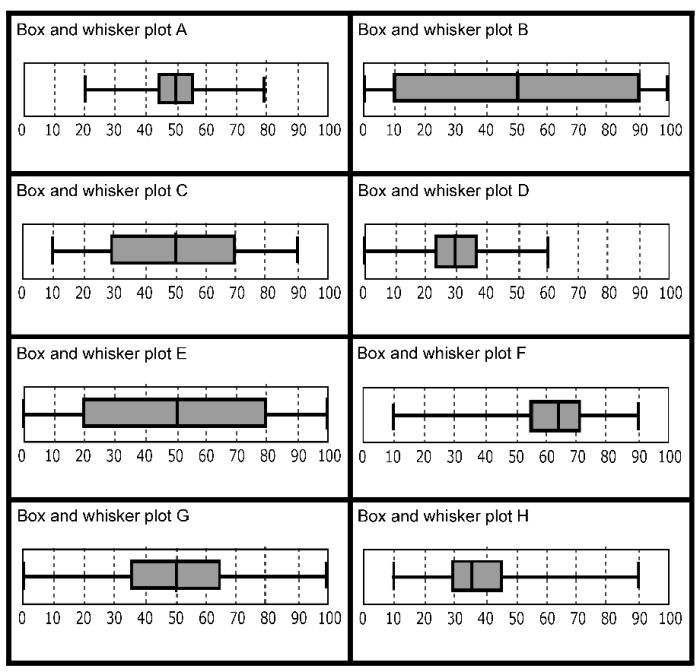
Box and whisker plots, also known as boxplots, are graphical representations of data that provide a concise summary of its distribution. They are widely used in statistics and data analysis to visually explore and compare datasets.
Box and Whisker Plot Basics
A box and whisker plot consists of the following components:
- Box:Represents the middle 50% of the data, known as the interquartile range (IQR).
- Median:A horizontal line inside the box that divides the data into two equal halves.
- Whiskers:Lines extending from the box to the minimum and maximum values of the data.
- Outliers:Individual data points that lie outside the whiskers, representing extreme values.
Creating Box and Whisker Plots
To create a box and whisker plot, follow these steps:
- Order the data from smallest to largest.
- Find the median, which is the middle value of the ordered data.
- Calculate the quartiles (Q1 and Q3), which divide the data into four equal parts.
- Draw a box from Q1 to Q3, with a line at the median.
- Extend whiskers from the box to the minimum and maximum values.
- Plot any outliers as individual points.
Interpreting Box and Whisker Plots
Box and whisker plots provide valuable insights into the distribution of data:
- Median:Indicates the center of the data.
- IQR:Measures the spread of the middle 50% of the data.
- Whiskers:Show the range of most data values.
- Outliers:Identify extreme values that may require further investigation.
Applications of Box and Whisker Plots, Box and whisker plot worksheet 2 answer key
Box and whisker plots are used in various fields, including:
- Data Analysis:Summarizing and comparing data distributions.
- Statistics:Identifying outliers, skewness, and kurtosis.
- Research:Exploring relationships between variables and testing hypotheses.
Interactive Box and Whisker Plot Tool
An interactive box and whisker plot tool allows users to:
- Upload or enter data.
- Generate box and whisker plots.
- Adjust settings to customize the plot.
- Export the plot as an image or data file.
Practice Problems and Solutions
Problem 1:Create a box and whisker plot for the following data: 10, 12, 15, 18, 20, 22, 25, 28, 30
Solution:Median: 19; Q1: 14; Q3: 25; IQR: 11; Whiskers: 10 to 30; Outliers: None
General Inquiries: Box And Whisker Plot Worksheet 2 Answer Key
What is the purpose of a box and whisker plot?
Box and whisker plots provide a graphical representation of data distribution, allowing for the identification of central tendencies, variability, and outliers.
How do I create a box and whisker plot?
Follow the step-by-step instructions provided in this guide, which include organizing data, calculating quartiles, and plotting the components of the box and whisker plot.
What information can be interpreted from a box and whisker plot?
Box and whisker plots reveal the median, quartiles, range, and presence of outliers, providing insights into the distribution and variability of data.